HuiLYue2023-08-31 21:15:31
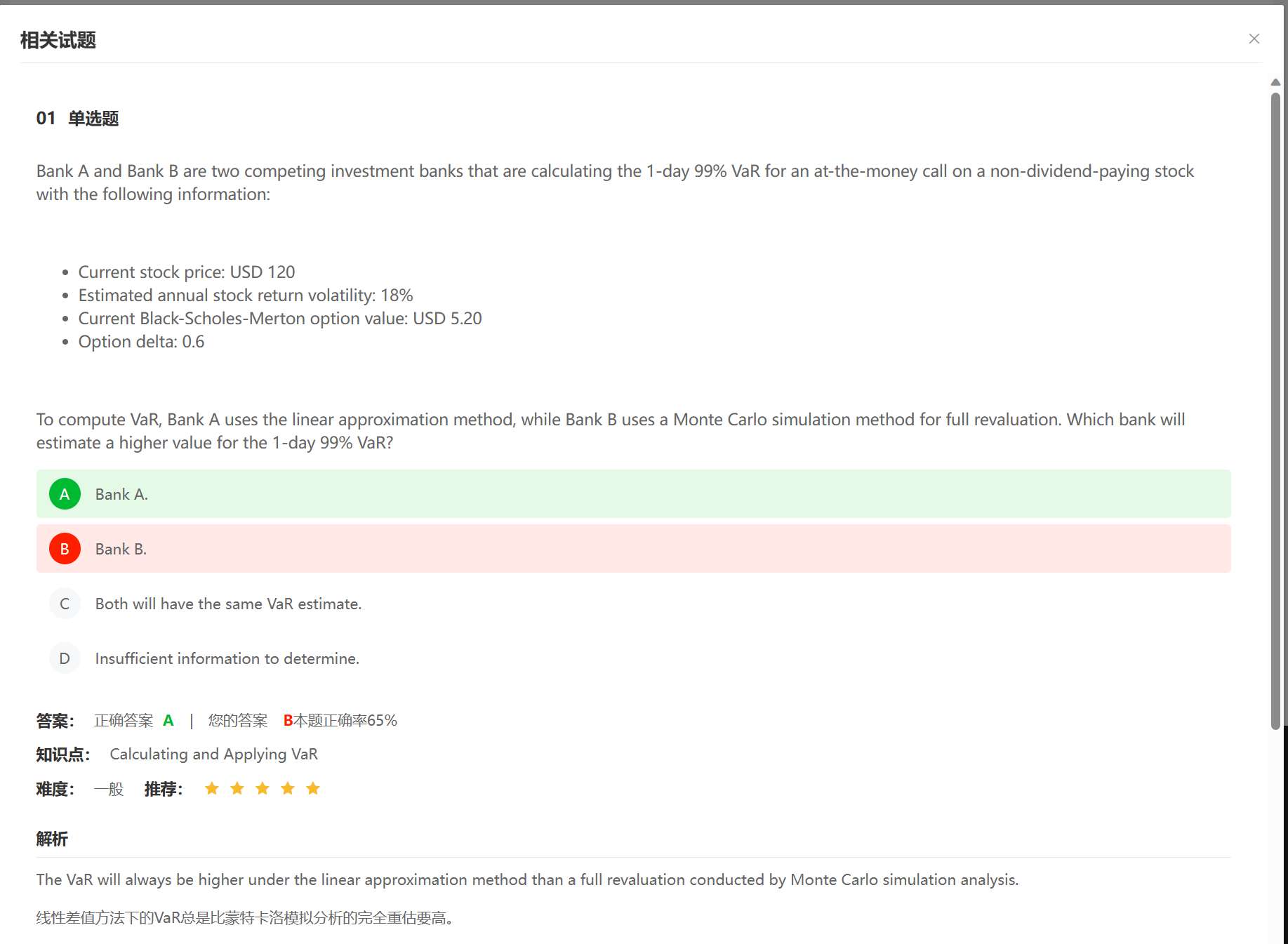
HuiLYue老师，这两道题放在一起应该怎么理解呀？使用局部数据的简陋delta-normal估计要大于使用全局数据高级的Monte Carlo Simulation估算出来的VaR值。。然后Monte Carlo随着实验的不断精进，样本n不断上升，会逐渐向上收敛于delta-normal法估算出来的Overestimate的不精准的VaR？
回答（1）
尹旭2023-09-01 09:26:18
尹旭同学你好，对于研究 VaR 的这两个方法的比较，思路是这样的。
1、 delta-normal 法是使用了风险因子的估计方法，首先肯定是不精确的，并且 delta-normal 只考虑了一阶线性风险因子的影响，没有刻画出债券或期权的二阶曲度特征，它的公式是 VaR(df)=IΔI x VaR(dS) （对于期权来说）。delta-gamma 法就考虑了二阶风险的影响，它的公式是 VaR(df)=IΔI x VaR(dS) — 0.5 x Γ x VaR(dS)^2，delta-gamma 法是更接近与真实价格的，但是它比 delta-normal 法算出来的值小。也就是说 delta-normal 法的结果会高估。
2、MC 法是不假设分布的估计方法，它也是估计，是对数值的模拟，但是它的结果与 delta-gamma 法更接近，因为也考虑了期权或债券的曲度特征（只要你输入的数据是真实数据，数据中就自然包含了曲度的特征，那模型算出来的数据也就会包含曲度特征），所以 delta-normal 法也会相对于 MC 法高估。
加油同学，老师与你一起乘风破浪。如果对答疑满意，别忘点个采纳哦~
- 评论（0）
- 追问（2）
- 追问
-
这个回答没解决我问题呀。。我问的是向上收敛的问题，这两道题结论完全相反
- 追答
-
同学你好，
这道题，如果将 delta - normal 法和 MC 法还有 HS法放在一起讨论的话，那 delta - normal 法就是个广义的概念，这里包含了 一阶 delta - normal和二阶 delta - gamma 的方法。
并且题目中已经说了 标的资产是服从正态分布的，那用 delta - normal 法就已经能很好估计标的资产的 VaR 值了（包含了考虑二阶曲度的影响），也就是结果会很贴近真实的 VaR 值。
而 MC 法随着 n 增加，结果会更加贴近真实的 VaR的结果。 delta - normal 法和 MC 法（n很大的情况下）都很贴近真实的 VaR的值了，所以两种方法的计算出来的结果就很趋同。
而你贴出来的图片中的题，它说了特指 delta - normal 法中 linear 的估计（只考虑一阶线性因素），那就是说没有考虑二阶曲度的影响，肯定就不精确。
评论
0/1000
追答
0/1000
+上传图片