尹旭2023-07-31 10:09:31

同学你好，要注意理解公式的推导过程。

威廉夏普在马科维茨的“有效前沿”的基础上，把无风险资产加入原来风险资产的分析框架中考虑。也就是把无风险资产看成一部分（收益率Rf，给它个权重Wa），把风险资产组合看成另一部分（收益率E(Rp)，权重就是1-Wa），来考虑这两部分的收益（ER）与风险（σ）。

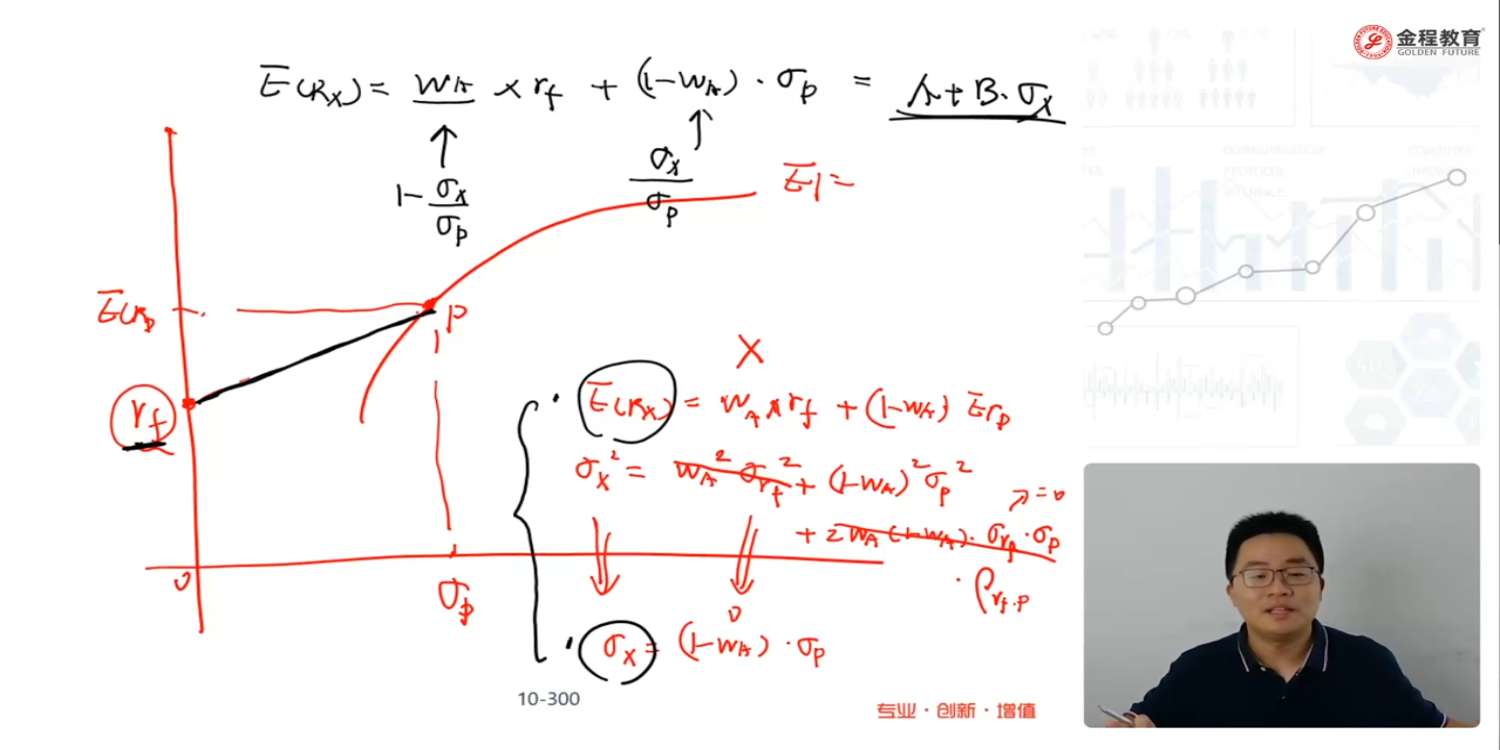
根据组合预期收益率的公式 E(R)=Wa × Rf + (1-Wa)  ×E(Rp)；（右上角确实是乘以 E(Rp) 而不是σp ）
根据组合标准差的公式 σx^2 = Wa^2 × σrf^2 + (1-Wa)^2 × σp^2 + 2Wa×(1-Wa)×σrf × σp× ρ，因为无风险资产的σ为0 （σrf=0，因为收益是确定的，不存在不确定性），所以公式中 Wa^2 × σrf^2=0，2Wa×(1-Wa)×σrf × σp× ρ=0，然后公式就只剩下 σx^2=(1-Wa)^2 × σp^2，两边同时开根号可得 σx =(1-Wa) × σp ，这就没有平方了，就是线性的，在图中就是一条直线。

然后根据 σx =(1-Wa) × σp 可知 Wa = 1- σx/σp，带入第一个公式 E(R)=Wa × Rf + (1-Wa)  ×E(Rp)，则有
E(R)=(1- σx/σp) × Rf + σx/σp  ×E(Rp)，这也是没有平方的，是线性的，也是一条直线。

加油同学，老师与你一起乘风破浪。如果对答疑满意，别忘点个采纳哦~