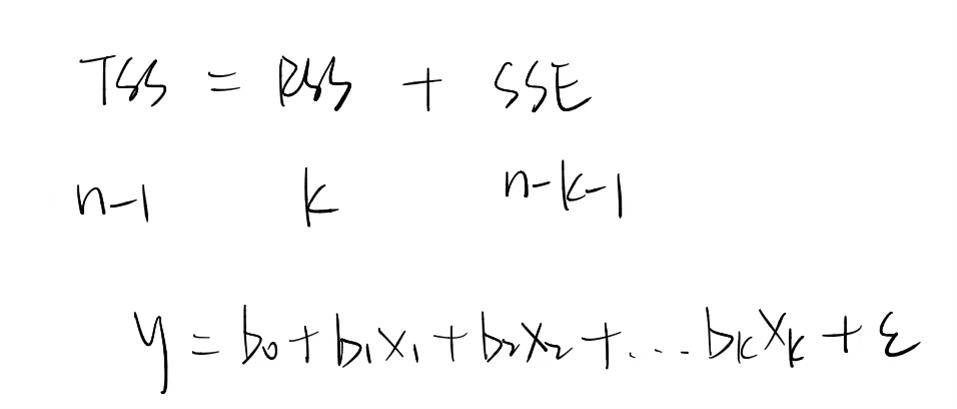Flower2021-10-17 17:10:22
Flower单元回归中自由度n-k-1的理解
回答（1）
Essie2021-10-18 10:08:20
Essie你好，自由度是取值不受限制的变量的个数。单元回归中，需要明确两个参数，即截距和斜率（b0,b1），才能确定残差项，因此自由度为n-2，如果存在多个自变量x，则存在多个斜率，因此其自由度本质为n-k-1，其中k代表自变量x的个数，1代表截距。换言之，自由度即为n减去参数的个数。加油~
- 评论（0）
- 追问（2）
- 追问
-
自由度是影响分布的形态么，比如T分布，对于同样的单元回归，如果样本量越大，那么自由度就越大。然后为啥老师会说n-k-1的意思是有k-1个值就可以确定其他的值？类似这样的意思哦，我有点记不清了
- 追答
-
你好，当样本容量较大，自由度也会随之增大，t分布会接近于正态分布。
根据下图，因为我们是用x去解释y，所以回归部分对应的自由度是自变量的个数k。
对于整体部分TSS，我们看的是y的自由度，如果有一组数据y，就可以得到y的均值。只要均值是确定的，那么只要知道样本中n-1个数，就可以求出第n个数字。举个例子：2 4 6这三个数字，均值为4。那如果我没告诉你第三个数字是6，只说了有三个数字，前两个是2和4，均值是4，你是可以计算出第三个数字的准确数值的，所以总体部分自由度n-1。
根据TSS=RSS+SSE，自由度也满足以上关系，所以SSE部分的自由度等于n-1-k 。
- 追答
-
你好，当样本容量较大，自由度也会随之增大，t分布会接近于正态分布。
根据下图，因为我们是用x去解释y，所以回归部分对应的自由度是自变量的个数k。
对于整体部分TSS，我们看的是y的自由度，如果有一组数据y，就可以得到y的均值。只要均值是确定的，那么只要知道样本中n-1个数，就可以求出第n个数字。举个例子：2 4 6这三个数字，均值为4。那如果我没告诉你第三个数字是6，只说了有三个数字，前两个是2和4，均值是4，你是可以计算出第三个数字的准确数值的，所以总体部分自由度n-1。
根据TSS=RSS+SSE，自由度也满足以上关系，所以SSE部分的自由度等于n-1-k 。
评论
0/1000
追答
0/1000
+上传图片