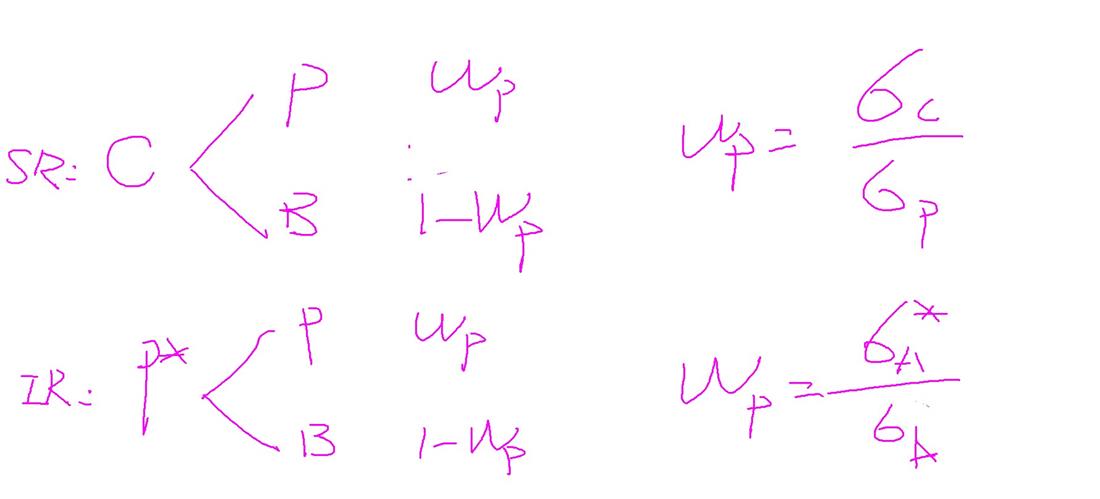李同学2020-10-30 13:31:44
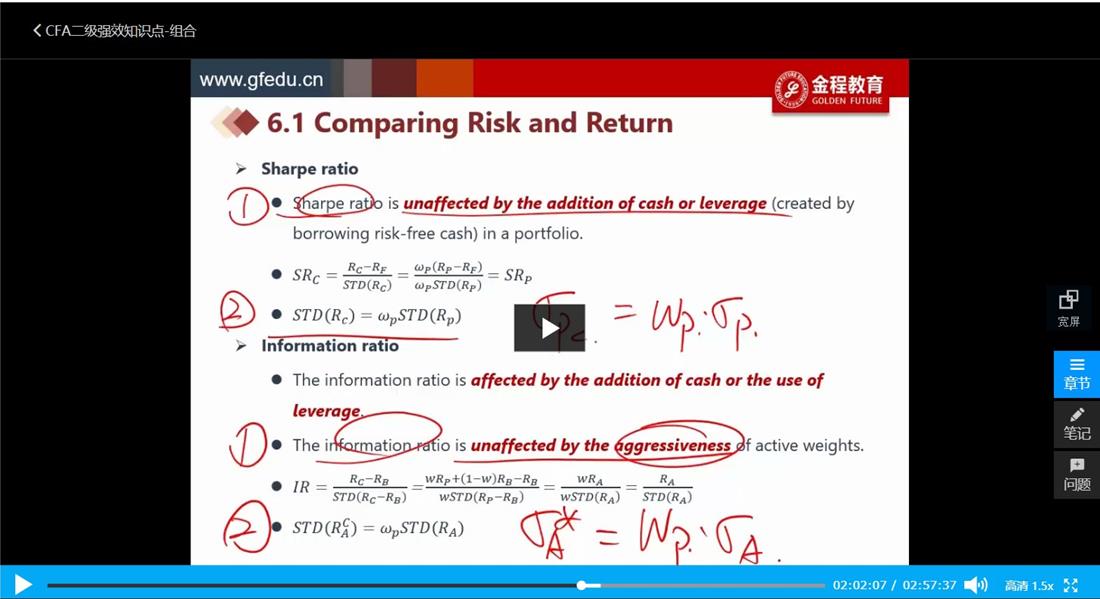
李同学组合 80知识点 36 如图2（我画的图 尽量描述的清楚一点：上面表示SR中一个新的portfolio的构建时算权重；下面表示IR中一个新的portfolio的构建时算权重）问题：1，我对比了一下，这里在求Wp（即：我想构建一个新的portfolio，那老的portfolio的权重应该配置多少呢），上面的公式和下面的公式的区别是什么？（我的理解：从公式上来看，上面的是组合本身回报率的标准差之比，下面的是组合的超额回报的标准差之比），不知道是否理解正确？2.如果理解正确，那为什么直接拿回报率算出来的和拿超额回报的算出来的结果会是一样的？
回答（1）
Johnny2020-10-30 15:11:23
Johnny同学你好
1.上面sharpe ratio中，新组合是由旧组合与现金（无风险资产）结合而成的，这样新组合的标准差是旧组合标准差乘以权重，而且新组合的夏普比率与旧组合相同，因为加入现金部位不影响夏普比率。所以你图中的SR画错了，C是由P和Rf（或者cash）组成，而不是由P和B组成。
下面的IR中，新组合是由旧组合与benchmark结合而成的，这样新组合的主动风险是由旧组合的主动风险乘以权重，而且新组合的信息比率与旧组合相同，因为aggresiveness的变动不影响信息比率。
这样应该就比较好理解了。
致正在努力的你，望能解答你的疑惑~
如此次答疑能帮助你理解知识点，可以通过【点赞】来让我们知晓。你的反馈是我们进步的动力，祝你顺利通过考试~
- 评论（0）
- 追问（6）
- 追问
-
老师您纠正的是对的。我想区分的是：上面的 σp是p组合的收益率和0(假设现金的收益率是0)轧差算出来的标准差；而下面的σA是p组合的收益率和benchmark的收益率轧差算出来的标准差。如果这样理解的话，二者其实是一致的，所以公式一样？我想问的点是 为啥公式会一样，明明一个SR，一个是IR.这样理解对否？
- 追答
-
同学你好
现金收益率绝对不是0，即使是无风险资产也会获得无风险收益率，所以现金最起码可以存银行赚无风险收益，但是现金收益率的标准差是0。
上面σc是p组合收益率的标准差与0进行加权平均得出的，因为现金是无风险资产，它的收益率的标准差为0，现金收益率与p组合收益率的相关系数为0，所以新组合的收益率标准差就是p组合的收益标准差乘以权重。
下面σA是p组合的主动风险与benchmark的主动风险加权平均得出的，而benchmark的主动风险为0，也就是说新组合的主动风险就是p组合的主动风险乘以它的权重。
所以这两者的公式是不同的，应用场景也是不同的，夏普比率对应于无风险收益率以及绝对风险，信息比率对应于benchmark以及主动风险。
致正在努力的你，望能解答你的疑惑~
如此次答疑能帮助你理解知识点，可以通过【点赞】来让我们知晓。你的反馈是我们进步的动力，祝你顺利通过考试~
- 追问
-
但二者想求的东西是相同的对吧？就是：就是我现在想用一个老组合和一个基准拼一个新组合，想求老组合在新组合中的占比？
- 追答
-
同学你好，你的理解是正确的
- 追问
-
我干脆这么记吧：这俩想要求的东西一样，公式也谁比谁也是没有区别。就是一个是SR，所以是组合的σ，一个是IR，所以是超额回报的σ。其实我已经记住了，其实还是不明白，为什么公式和想要求的完全一样，但是一个是σp 一个是σA,不想推导了，不过还是冥冥中感觉在某种条件下两个东西可以证明是一个东西？
- 追答
-
同学你好，公式是不一样的，应用的场景也是不一样的，但是求的东西是一样的，都是p组合的权重。如果你有最理想的新组合的回报标准差，就可以得知p组合与现金的配比；如果你有最理想的新组合的主动风险，就可以得知p组合与benchmark的配比
评论
0/1000
追答
0/1000
+上传图片