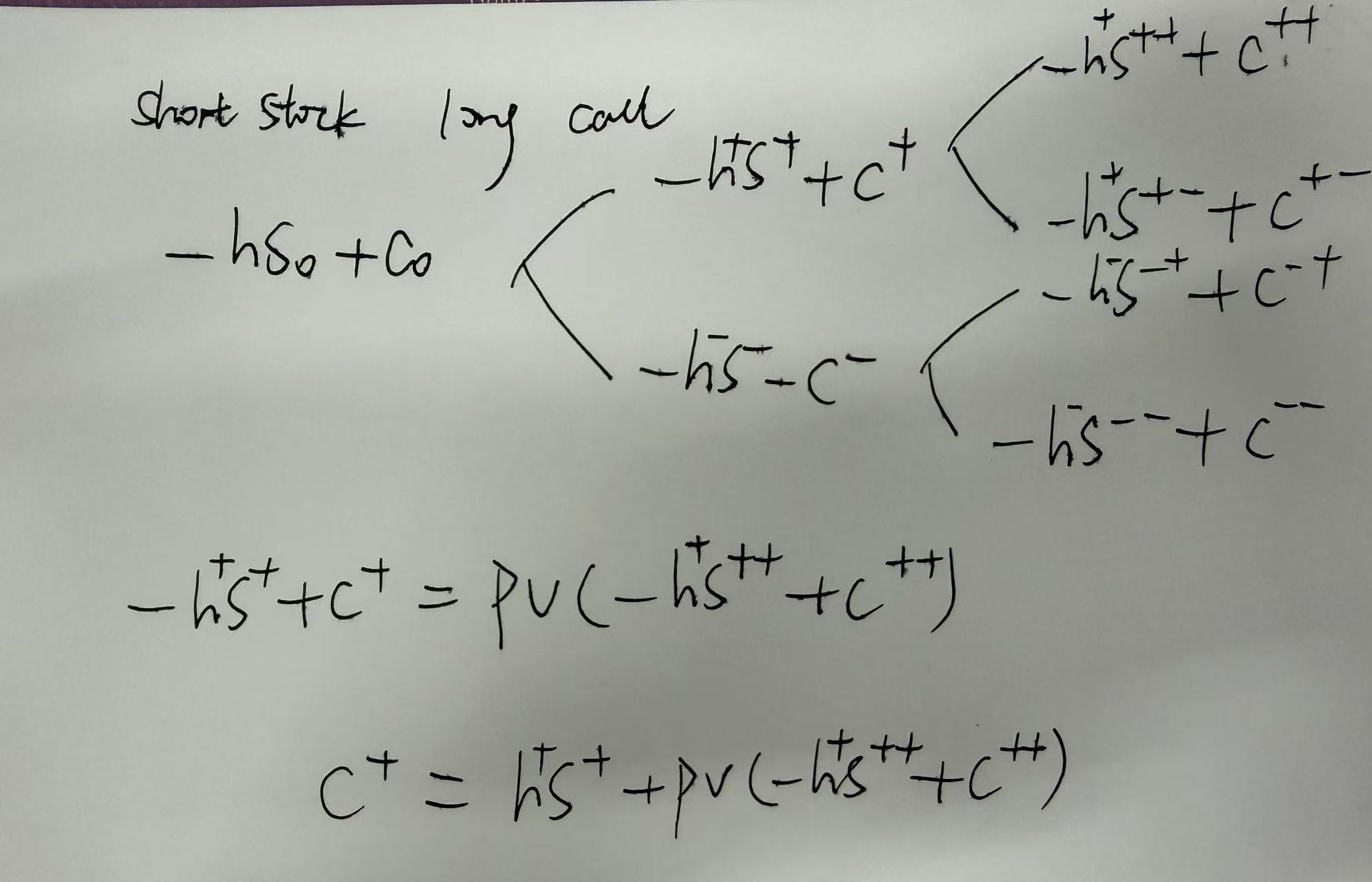112025-10-12 12:25:59
11图一中，红线的部分是什么意思? 既不考虑未来发生的可能性，也不考虑所有可能的结果，但最后的数值却诡异的相等，比如Cu = delta up ×uS + PV(delta up× udS + Cud), 考虑现金流时，call 在t=1 的节点 在t=2 向下走(C+-, S+-; C--, S--)，put 在t=1 的节点就向上走(P++, S++; P-+, S-+)
回答（1）
Essie2025-10-13 16:50:54
Essie同学你好，只有expectation model里才需要考虑风险中性概率。
无套利模型本来就不要考虑概率。无套利模型通过拿股票和期权，构建一个完全对冲的投资组合，未来股价上升还是下跌，组合的价值都不变，未来一年的组合价值和前一年的组合价值只差一个无风险收益。
所以截图上面用看涨期权构建无套利组合时，是short stock，long call。
下面用看跌期权构建无套利组合时，是long stock和long put。
以short stock，long call举例，见下图，我们就拿两年都上涨来举例，可以参照下图公式。
这个无套利模型和用风险中性概率最后计算出来的结果本来就是一样的。
- 评论（0）
- 追问（2）
- 追问
-
你好，这里对冲不是购买delta个股票吗？为什么是delta + gamma？
- 追答
-
因为Delta衡量的是期权价格对标的资产价格变化的一阶敏感度，而Gamma衡量的是这种敏感度本身随价格变化的快慢。用Delta对冲可以消除一阶价格风险，但当股价波动较大时，Delta会不断变化，此时仅靠Delta对冲会产生误差。
为了更精确地对冲，需要同时考虑Gamma，对冲掉Delta的变化风险。在一般考试或题目中，我们通常只考虑Delta对冲即可。
评论
0/1000
追答
0/1000
+上传图片