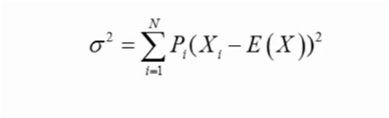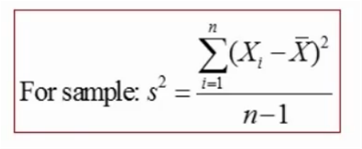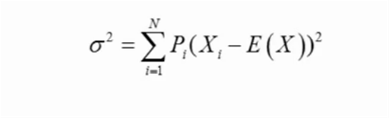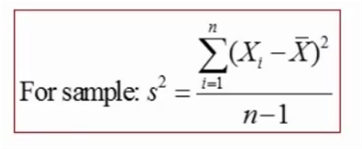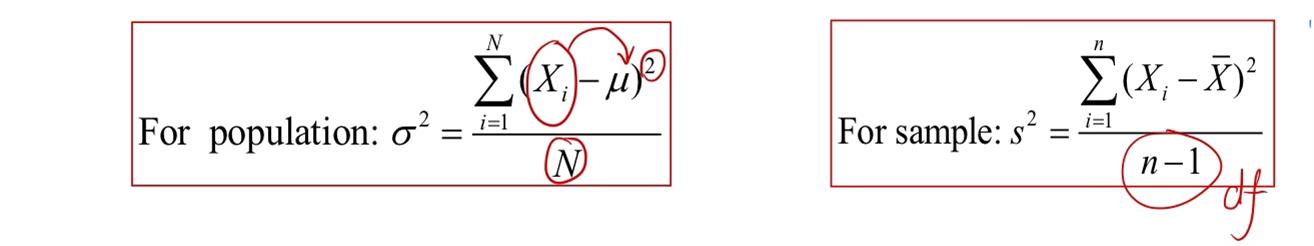IVY Wang2019-11-26 23:11:21
IVY Wang你好，请问这个课件里提到的方差，与之前学到的几个方差公式（分母是N与N-1）有什么区别？又分别对应于怎样的实际应用呢？不太明白。谢谢
回答（2）
Evian, CFA2019-11-27 11:12:01
Evian, CFAIVY Wang同学你好，
嗯嗯～数量中确实出现了很多个方差的公式。
可以麻烦你截图指明是哪一个公式么，我不知道你说的具体公式，谢谢～
- 评论（0）
- 追问（3）
- 追问
-
比如这两个，结合实际应用，针对的含义是什么？又都怎样应用呢？谢谢
- 追问
-
上一个图片好像有点问题
- 追答
-
第一个公式里面，Pi使得应用范围更广~
一组数据是否是总体或者是样本，取决于研究的主体是什么，“研究全班人身高”全班人身高就是总体，“研究全国人身高”全班人身高就是样本~
第一个公式确实可以应用于总体和样本~
第二个公式仅仅用于样本~（和附图一起记忆比较好）
Bingo2019-11-27 17:51:49
Bingo同学你好。第一个公式是针对一组随机变量的方差。方差的本质就是求期望，而随机变量的期望本质就是求加权平均。只不过，这里求加权平均的对象是：(X-EX)²。
第二个公式针对一组数据，这个数据是随机抽取的一组样本，此时可以直接用这个公式求出样本的方差。
其实两个公式本质一样的，只不过第一个用的是概率的思想在算。
- 评论（0）
- 追问（3）
- 追问
-
老师好。可以麻烦进一步拓展一下你这里提出的“一组随机变量”和“一组数据”的区别吗？这一组数据也是随机抽取的啊，是不是可以理解成是随机的呢？谢谢
- 追答
-
同学你好。一组数据不一定就是样本，可能是总体。
比如抛筛子，只有6个面，总共就6个数据。
- 追问
-
可以理解成第一个公式应用范围更广一些吗？选中的一组随机变量有可能是总体，也有可能是样本，所以第一个公式对于样本和总体的情况都可以应用。但是第二组只可以用于样本？
评论
0/1000
追答
0/1000
+上传图片