Evian, CFA2019-08-29 10:33:06

詹同学你好，

t学生分布和正态分布比较时，他们的方差是不同的，所以此时的T分布是低峰肥尾。

而在你的截图里，此时相比于正太分布，这个高峰瘦尾分布也是正确的。在这种情况下：
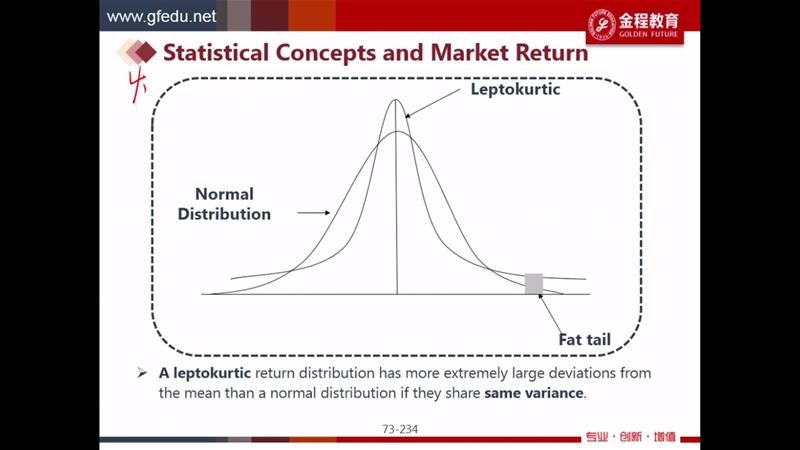
为什么高峰等价于肥尾呢？这里有一个前提条件，所要研究的分布与正态分布的方差相同（截图汇最后有一个“same variance”信息），即两组数据通过方差衡量出的离散程度相同。若所要研究的分布为高峰，说明这组数据在靠近均值的部分数据多，分布比较集中。为了保证总体的离散程度相同，则在远离均值的地方分布必须比较松散，即极值出现的可能性比较高，所以会出现“肥尾”的现象。

同理，当所研究的分布与正态分布的方差相同时，如果所要研究的分布为低峰，说明靠近均值的部分数据少，分布比较松散。为了保证总体的离散程度相同，则在远离均值的地方分布必须比较紧密，即极值出现的可能性要比较低，所以会出现“瘦尾”的现象。